The heat capacity of a diatomic gas is
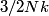 in the limit of low temperatures. As the temperature is increased, rotational modes eventually become active and add in the limit of low temperatures. As the temperature is increased, rotational modes eventually become active and add 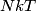 to the heat capacity, making the total heat capacity equal to to the heat capacity, making the total heat capacity equal to 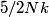 . This occurs at a temperature well below room temperature. As the temperature increases well above room temperature, vibrational modes also become active and also add . This occurs at a temperature well below room temperature. As the temperature increases well above room temperature, vibrational modes also become active and also add 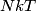 to the heat capacity, making the total heat capacity equal to to the heat capacity, making the total heat capacity equal to 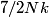 . So the ratio of the heat capacity at very high temperatures to the heat capacity at very low temperatures is: . So the ratio of the heat capacity at very high temperatures to the heat capacity at very low temperatures is: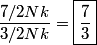 Thus, answer (D) is correct. |